vorticaddy.blogg.se - Altitude geometry right triange

Thankfully, we know the length of the other piece so all that's left is adding them together.ĭone. We wanted to know the length of the hypotenuse of the biggest triangle, but 18 is only a piece of it. If we divide both sides by 8, we can figure out the mysterious a's real identity: 18. The altitude is also the long side of the bottom triangle, and the smaller piece of the hypotenuse is the short side. The unknown piece, which we'll call a (because it refused to tell us its real name), is the long side of the top triangle, and the altitude is the short side. Setting up our proportion is a good place to start. We already know that 8 is the smaller piece (but we won't tell it because we don't want to hurt its feelings), so all we have to do is find out what the bigger piece is. We want to find the length of the biggest triangle's hypotenuse. If we have the right information, we can find the length of any side of any triangle. Everest, but it's a start. We can use these proportions to solve for more than just the length of the altitude. Hopefully it's a smallish number, or else we may get lightheaded. If we substitute those numbers into our proportion, we can solve for the length of the altitude. What is the length of the altitude of this triangle? We're still doing math, so why don't we throw some numbers up in here? Sample Problem

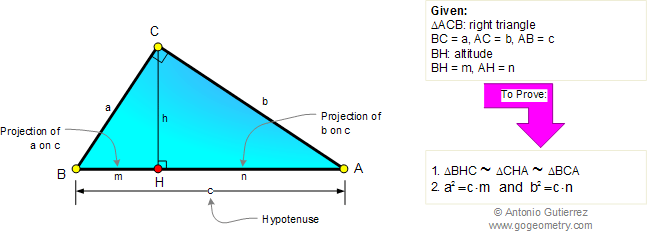
The next step is actually solving these bad boys. If the shortest side of the first triangle is in the denominator, ditto for the second. That means if a hypotenuse is in the numerator of one fraction, another hypotenuse should be on the numerator of the other.

Different triangles are separated by the equal sign.

The type of side is separated by the fraction.

Two things to remember about these proportions: She'll swoon at your knowledge of geometric means and maybe even pay for your Coca-Cola. So you can find out Aybeesee's height no problem. Whaddayaknow? It's the same proportion as the geometric mean. Aybeesee's height is the short side of one baby triangle and the long side of the other baby triangle.Ĭompare the short side to the long side of each triangle and set them equal to each other. If we want to find Aybeesee's height, we can use the similarity of the triangles and make a proportion out of the sides. The "identical angles" kind of similar, not the "Mary-Kate and Ashley Olsen" kind of similar. They might be different sizes, but these three right triangles are all similar. Knowing that, there's a possibility that Aybeesee is really two baby triangles in a cocktail dress. This line, called the altitude, splits her into two smaller right triangles. Well, her height is the length from point A, where her 90° angle is, down toward her hypotenuse at point D. She's a supermodel, so she's really proud of her height.

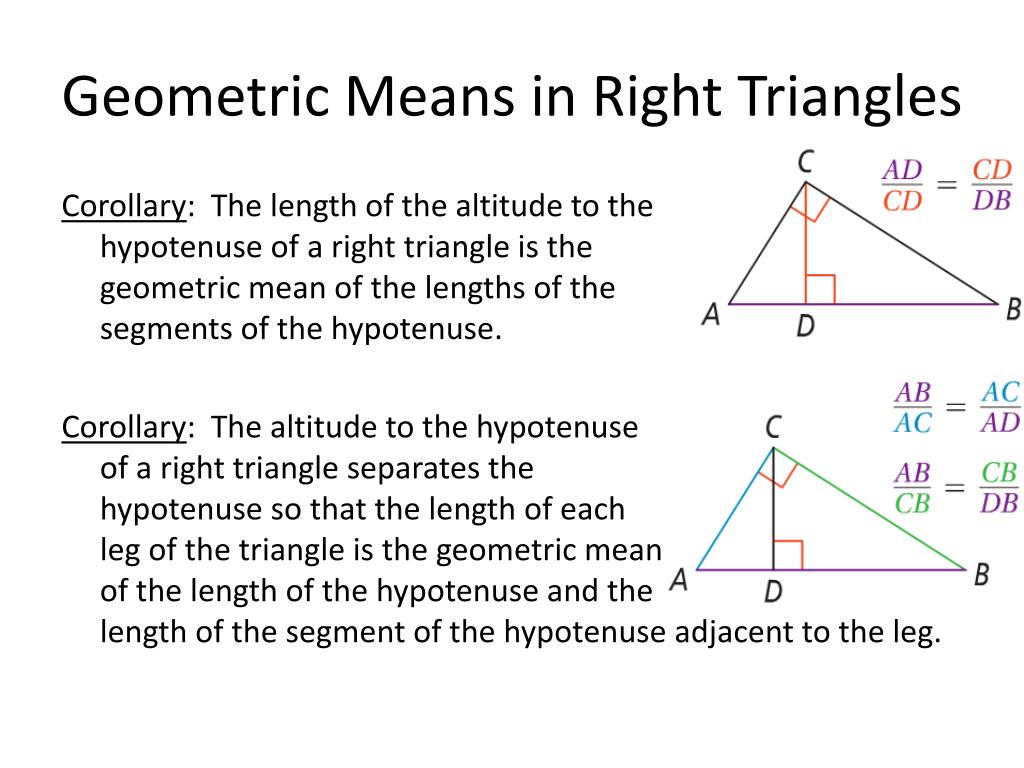
Say that a triangle at the bar, named Aybeesee (or ABC for short), wants you to guess her height. Why would a right triangle ask you about geometric means? More importantly, how would a right triangle ask you about geometric means? Take the square root, and you're back to square one. If we cross-multiply, we can solve for the geometric mean and it'll give us the definition.

Now, the reason this is helpful is because it lets the triangle know you care, and it comes from a proportion that looks like this: So if you're ever at a bar (drinking a Coca-Cola or chocolate milk, of course) and a right triangle asks you to find the geometric mean of 4 and 16, you won't break a sweat. Just multiply two numbers together and take the square root. To find altitudes of unruly triangles, we can just use the geometric mean, which actually isn't mean at all.